这个是一个让人感觉很神异的技术,给一堆图片,然后用软件扫描,软件就能把图片中的特征找出来,这对人来说是很轻易的事,对软件来说,最大的问题就是,怎么应该进行才可以?
写软件的技术也不是多么高科技,最终需要用到的还是人的思想,然后把思想转化成代码,从而解决现实问题,编程可以说是一个验证思路的一个绝佳途径,在下甚至以为,新时期的道士,应该个个都掌握编程的技能。
说远了。
这个给了一堆图片,然后能提取出特征,应该怎么实现?
一般的问题想要智能解决,思路是这样的:给一组输入,再给一组输出,比如天气预报,输入的就是时间,输出就是天气,然后给神经网络任意赋上一堆值,再通过数学运算,看目标结果与需要的输出数据相差有多大,然后转化成微积分的方向,计算出运算路径中应该怎么反向调整数据才能拼凑出目标结果来,然后不断重复这个计算并再拼凑的过程,最后接近目标结果,得到满意答案而确定出来的神经网络中的参数,就可以理解为特性。
但是如果是一堆图片,这个怎么处理?如何提取图片中的特征,这里不得不说,有一个很有意思的解决方案。
它是这样进行的:
1、把图片切成各种小块,并把这些小块换成数据表达
2、用神经网络去运算这些数据
但问题来了,运算的数据的输出结果是什么?
这里就是极其聪慧的一点啊,输出的结果再进行一次神经网络运算,让它能输出为输入值。
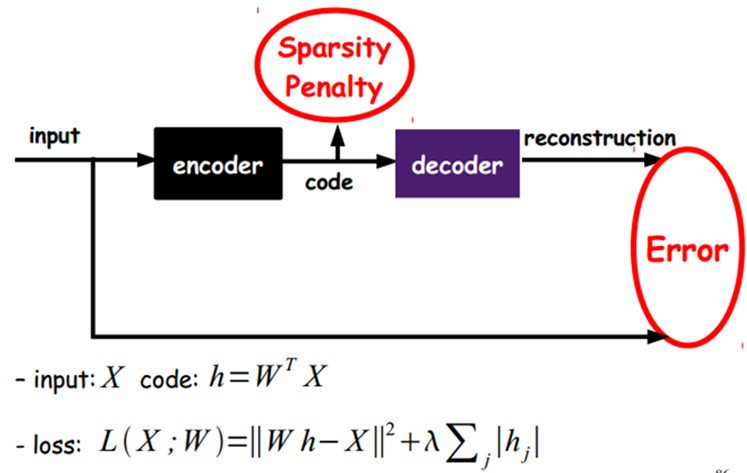
输入-》运算(编码)-》运算(解码)-》输出
然后比较输入与输出,根据差值,去调整中间的编码运算与解码运算,而至于编码与解码到底在干什么是不用管的。
反正最后输入与输出结果精度达到满意要求时,所保留的就是特征了。
为什么会这样?其实原理很简单,中间的编码层的神经网络处理,相当于去将原图进行任意的干扰,而解码层的神经网络处理,相当于将干扰后的图像进行了恢复。
而这个过程有一个有意思的地方是,因为中间出现了干扰与解干扰的过程,输出等于了输入,多次变换后,保留下来能识别到原输入的就是特征。
同样的,可以在这种思路中,多加入一个混淆器,即随机添加大量的噪音,然后再消除掉,同样可以增强神经网络的搞干扰能力,而进行了干扰处理后的这种手法得到的编码器称为Denoising AutoEncoders降噪自动编码器。
这真是一个令人惊叹的想法,而且只能在计算机上实现,传统的其它计算工具是无法实现这个的,因为它依赖大密度的运算。
那么这样就够了么?
于是这里出现一种信念,这种特性的抽象是否可以尽量的简单再简单?
损之又损,以至于无为,无为而无所不为?
这个可能吗?
于是,如果坚持相信,再复杂的东西背后都有简单的规则的话,这里就可以基于这种信念再干一件事:稀疏化
怎么做呢?因为复杂的背后总有简单的规则是不是?那么简单的规则是不是就意味着可以删减很多东西后,还只保留最核心的一些东西,就能复原绝大部分原来的信息?
既然是这样,那么就意味着,如果能找到一种,让神经网络里大部分神经元不起作用也能进行成功由输入得到输出结果时,那么就能得到这个。
所以,可以对神经元进行限制,每个神经元有一个激活值,然后规定所有的神经元的总激活值,不得超过一个数值,比如0.05,那么这样就会导致大部分神经元变成0值,而极少数神经元需要更加精准的计算出自己的权值。
那这个怎么实现?
先从源头说起,稀疏化,实际上就是寻找一组“超完备”基向量来更高效地表示样本数据。稀疏编码算法的目的就是找到一组基向量 ,使得我们能将输入向量表示为这些基向量的线性组合。
首先,输入与输出必须要满足:Min |I – O|,其中I表示输入,O表示输出,即输入与输出相差小值。
如果用图片来说,就是能找到少量的、微小的图片来组合成这个大图,然后这堆微小的图片,称它为字典Φ,而任意抽一个小图片出来(比最微小的图片要大),那么这个小图片,就全塞进去,因为还可以比如是Φ1的20%与Φ2的50%与Φ3的50%共同构成了这个图(因为比最小图片大,所以加起来会超过100%)。
那么因为“要找到最小图片”所以就等于是加上了一个多的条件限制,因为O为输出,O就是那个抽出来的那个图需要求的目标图,而输入为I,所以就可以表达为:
I=x1+x2+x3+x3…..xi
O = a1Φ1 + a2Φ2 + … +anΦn
然后考虑加入一个惩罚系数,这个用于调节网络里的值用。
那么实际上解决问题就是要把a和Φ拼凑出来,使得计算结果变成一个最小值。
右边加号后的就是加入的稀疏代价函数,这个函数也可以用对数代价函数(利用柯西先验概率),即log(1+ai2),它是用来对于远大于零的值进行限制用的,以避免出现网络中的值相差太大并集中,从而失去了稀疏化的目的。
因为目标最小值是稳定的,如果Φ或a中的值太大了的话,右边的代价函数就没什么意义了---会变得非常小。所以要对||Φ||2的值进行限制,让它小于某个值。
在实现中,每次迭代分两步:
a)固定字典Φ[k],然后调整a[k],使得上式,即目标函数最小(即解LASSO问题)。
b)然后固定住a [k],调整Φ [k],使得上式,即目标函数最小(即解凸QP问题)。
然后就这样反复计算就可以了。
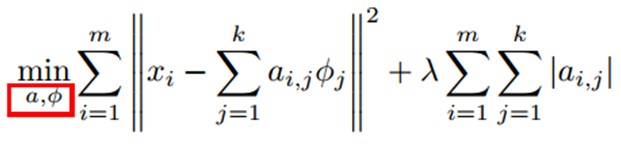
发表评论