一般的解释,傅立叶变换一个是在时域,一个是在频域,而时域与频域是不同的观察角度。
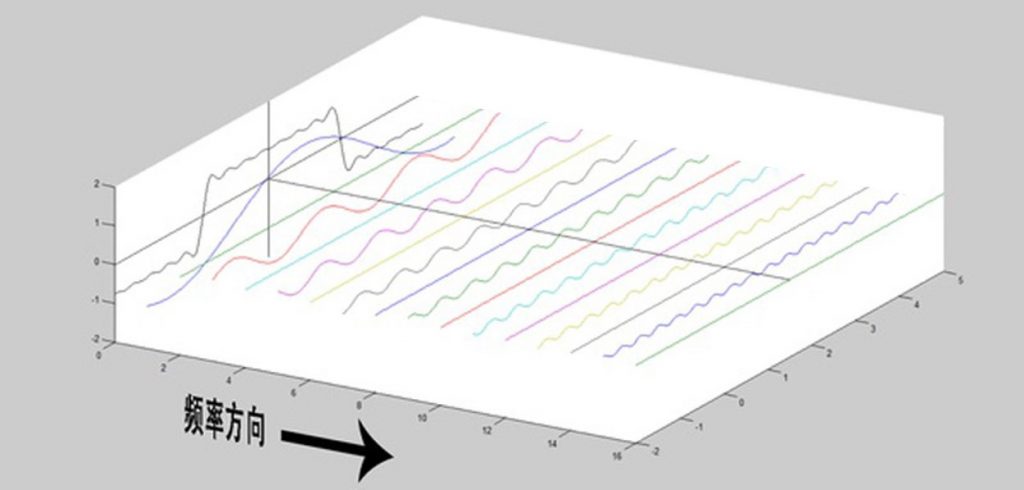
但有一个直观上不容易理解的问题是,为什么这种变换是可行的。比如当人看到一个3维物体时,不同的角度看到的都是一个切面,而仅仅是一个切面是无法包括所有的信息的。
观察角度的变化会不会造成信息的丢失?实际上,这是肯定会导致信息丢失的。
理想中如果一个信号的描述密度是无限大,那么必然也需要无限大的正余弦函数去进行模型才能办到。
但这里有一个巧妙的是,从某种意义上说,所有的信号,虽然我们看到的有光滑的曲线,但实际上是这个曲线是通过采样数据点进行连接出来的,只是对被观测的目标进行了一个近似的模拟。
假如有一个超级显微镜,可以无限放大所观察的目标,但由于受到物理世界的限制,因此最多也只能观察到到普朗克常量长度单位的尺度,如果再往下是无法进行观察的,因为宏观的物理意义会失效。
现实应用中我们对信号的采集密度比这个要远远小得多。
比如音乐,无限度的提高采样率其实并没有意义,因为人类的听力是有极限的,大体来说,如果将一秒钟的音乐分割为20000等分以上时,人耳就听不出其质量上的差异了,所以数字音乐通常选择44.1KHz的频率,已经超过了人耳的极限。
但这只是数据上的,如果将一个数字音乐还原成现实的声音的话,因为声音是由振动实现的,因此需要将这个频率以振动空气的方式表现出来,器材的不同所能还原的能力也不同。
同样的,用于对事物的分析的时候,有时候也不需要过于精细的粒度,根据描述的重点的需求不同,往往简单的一个采样描述就足够对事物进行一个勾勒。
正如,要画一个太阳,一般的常用做法,只需要画一个圆,而要描述地球与太阳 的轨迹,可以近似的画一个地球围绕太阳正圆转一圈,如果要进行更仔细的分析时,那么会将这样的轨道画为椭圆形。
所以傅立叶变换的要求就很明确了,也就是著名的狄利克雷条件,所要求的其实信号中的最大小值不能是无限的,如果有间断点必须是有限的,还有同一周期内必须是可积分的。
这里有一个非常巧妙的事情是,从频率角度来看,很多时候自然界的事物会符合一定的分布规律,比如像正态分布,往往就会成为一个曲线,而曲线可以通过简单的公式描述实现,因此这就为采用少量信息描述大量信息提供了一个很好的手段。
在传统的术数中也是一样,为什么要通过圆描述模型,因为这样才能将事情发生的频率归纳出来,这里会产生一个非常有趣的现象,虽然看起来是要选择一个视角去观察同类事物发生的频率,但另一方面这种视角的选择像是自然发生的,因为事物按照不同的特征提取方式,就会自发形成聚类的情况。
发表评论