Nine-Palace Rotation 1,8,3,4,9,2,7,6, calculate the sequence formula for this periodic sequence, the result is very complicated:
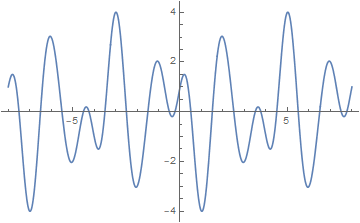
1/8 cos(1/4 π (n - 8)) + 1/8 cos(1/2 π (n - 8)) + 1/8 cos(3/4 π (n - 8)) + 1/8 cos(π (n - 8)) + 1/8 cos(5/4 π (n - 8)) + 1/8 cos(3/2 π (n - 8)) + 1/8 cos(7/4 π (n - 8)) + 1/4 cos(1/4 π (n - 7)) + 1/4 cos(1/2 π (n - 7)) + 1/4 cos(3/4 π (n - 7)) + 1/4 cos(π (n - 7)) + 1/4 cos(5/4 π (n - 7)) + 1/4 cos(3/2 π (n - 7)) + 1/4 cos(7/4 π (n - 7)) - 3/8 cos(1/4 π (n - 6)) - 3/8 cos(1/2 π (n - 6)) - 3/8 cos(3/4 π (n - 6)) - 3/8 cos(π (n - 6)) - 3/8 cos(5/4 π (n - 6)) - 3/8 cos(3/2 π (n - 6)) - 3/8 cos(7/4 π (n - 6)) + 1/2 cos(1/4 π (n - 5)) + 1/2 cos(1/2 π (n - 5)) + 1/2 cos(3/4 π (n - 5)) + 1/2 cos(π (n - 5)) + 1/2 cos(5/4 π (n - 5)) + 1/2 cos(3/2 π (n - 5)) + 1/2 cos(7/4 π (n - 5)) - 1/8 cos(1/4 π (n - 4)) - 1/8 cos(1/2 π (n - 4)) - 1/8 cos(3/4 π (n - 4)) - 1/8 cos(π (n - 4)) - 1/8 cos(5/4 π (n - 4)) - 1/8 cos(3/2 π (n - 4)) - 1/8 cos(7/4 π (n - 4)) - 1/4 cos(1/4 π (n - 3)) - 1/4 cos(1/2 π (n - 3)) - 1/4 cos(3/4 π (n - 3)) - 1/4 cos(π (n - 3)) - 1/4 cos(5/4 π (n - 3)) - 1/4 cos(3/2 π (n - 3)) - 1/4 cos(7/4 π (n - 3)) + 3/8 cos(1/4 π (n - 2)) + 3/8 cos(1/2 π (n - 2)) + 3/8 cos(3/4 π (n - 2)) + 3/8 cos(π (n - 2)) + 3/8 cos(5/4 π (n - 2)) + 3/8 cos(3/2 π (n - 2)) + 3/8 cos(7/4 π (n - 2)) - 1/2 cos(1/4 π (n - 1)) - 1/2 cos(1/2 π (n - 1)) - 1/2 cos(3/4 π (n - 1)) - 1/2 cos(π (n - 1)) - 1/2 cos(5/4 π (n - 1)) - 1/2 cos(3/2 π (n - 1)) - 1/2 cos(7/4 π (n - 1)) Simplify, available:
1/2 Cos[n π] ((1+Sqrt[2]) Cos[(n π)/4]-(-1+Sqrt[2]) Cos[(3 n π)/4]+3 (1+Sqrt[2]) Sin[(n π)/4]+3 (-1+Sqrt[2]) Sin[(3 n π)/4]) If we want to be in the palace, trying to calculate the innate gossip sequence is also very complex, will become like the following:
(-3 Cos[((-8 + n) Pi)/4])/8 - (3 Cos[((-8 + n) Pi)/2])/8 - (3 Cos[(3 (-8 + n) Pi)/4])/8 - (3 Cos[(-8 + n) Pi])/8 - (3 Cos[(5 (-8 + n) Pi)/4])/8 - (3 Cos[(3 (-8 + n) Pi)/2])/8 - (3 Cos[(7 (-8 + n) Pi)/4])/8 + (3 Cos[((-7 + n) Pi)/4])/8 + (3 Cos[((-7 + n) Pi)/2])/8 + (3 Cos[(3 (-7 + n) Pi)/4])/8 + (3 Cos[(-7 + n) Pi])/8 + (3 Cos[(5 (-7 + n) Pi)/4])/8 + (3 Cos[(3 (-7 + n) Pi)/2])/8 + (3 Cos[(7 (-7 + n) Pi)/4])/8 - Cos[((-6 + n) Pi)/4]/2 - Cos[((-6 + n) Pi)/2]/2 - Cos[(3 (-6 + n) Pi)/4]/2 - Cos[(-6 + n) Pi]/2 - Cos[(5 (-6 + n) Pi)/4]/2 - Cos[(3 (-6 + n) Pi)/2]/2 - Cos[(7 (-6 + n) Pi)/4]/2 - Cos[((-5 + n) Pi)/4]/8 - Cos[((-5 + n) Pi)/2]/8 - Cos[(3 (-5 + n) Pi)/4]/8 - Cos[(-5 + n) Pi]/8 - Cos[(5 (-5 + n) Pi)/4]/8 - Cos[(3 (-5 + n) Pi)/2]/8 - Cos[(7 (-5 + n) Pi)/4]/8 - Cos[((-4 + n) Pi)/4]/4 - Cos[((-4 + n) Pi)/2]/4 - Cos[(3 (-4 + n) Pi)/4]/4 - Cos[(-4 + n) Pi]/4 - Cos[(5 (-4 + n) Pi)/4]/4 - Cos[(3 (-4 + n) Pi)/2]/4 - Cos[(7 (-4 + n) Pi)/4]/4 + Cos[((-3 + n) Pi)/4]/2 + Cos[((-3 + n) Pi)/2]/2 + Cos[(3 (-3 + n) Pi)/4]/2 + Cos[(-3 + n) Pi]/2 + Cos[(5 (-3 + n) Pi)/4]/2 + Cos[(3 (-3 + n) Pi)/2]/2 + Cos[(7 (-3 + n) Pi)/4]/2 + Cos[((-2 + n) Pi)/4]/4 + Cos[((-2 + n) Pi)/2]/4 + Cos[(3 (-2 + n) Pi)/4]/4 + Cos[(-2 + n) Pi]/4 + Cos[(5 (-2 + n) Pi)/4]/4 + Cos[(3 (-2 + n) Pi)/2]/4 + Cos[(7 (-2 + n) Pi)/4]/4 + Cos[((-1 + n) Pi)/4]/8 + Cos[((-1 + n) Pi)/2]/8 + Cos[(3 (-1 + n) Pi)/4]/8 + Cos[(-1 + n) Pi]/8 + Cos[(5 (-1 + n) Pi)/4]/8 + Cos[(3 (-1 + n) Pi)/2]/8 + Cos[(7 (-1 + n) Pi)/4]/8This is actually the use of trigonometric functions to reflect the periodic function, was transformed, a total of 54, if only half of the description of the graph, they are only 180 degrees upside down, so consider the four sets of hexagrams order and set:
A=Cos[1/2π(-4+x)] B=Cos[π(-4+x)] C=Cos[3/2π(-4+x)] D=Cos[1/2π(-3+x)] E=Cos[π(-3+x)] F=Cos[3/2π(-3+x)] G=Cos[1/2π(-2+x)] H=Cos[π(-2+x)] I=Cos[3/2π(-2+x)] J=Cos[1/2π(-1+x)] K=Cos[π(-1+x)] L=Cos[3/2π(-1+x)]
Obviously, from A to L, it can be preliminarily thought that the description in 12 dimensions is obtained by taking 1 / 2,1,3 / 2 from x-1, x-2, x-3 and x-4, respectively, Since the final result is from -4 to 4 and the maximum value of 3/2 is 1.5, it is equivalent to a small piece divided into a plurality of 0 to 1.5, so that two to three are 1.5 values can constitute the fluctuations between 3 and 4.5, and then there are two amendments should be sufficient to express, so the reduction can be to four to five items, however, the reduction is not conducive to the observation of the internal structure, not simplified here .
坎艮震巽= -1 -1/4A-1/4B-1/4C-1/2D-1/2E-1/2F+3/4G+3/4H+3/4I-J-K-L 离坤兑乾= 1 +1/4A+1/4B+1/4C+1/2D+1/2E+1/2F-3/4G-3/4H-3/4I+J+K+L 震巽离坤=-(1/2) -3/4A-3/4B-3/4C+D+E+F-1/4G-1/4H-1/4I-1/2J-1/2K-1/2L 兑乾坎艮= 1/2 +3/4A+3/4B+3/4C-D-E-F+1/4G+1/4H+1/4I+1/2J+1/2K+1/2L 巽离坤兑=1/2 +1/2A+1/2B+1/2C-3/4D-3/4E-3/4F+G+H+I-1/4J-1/4K-1/4L 乾坎艮震=-(1/2) -1/2A-1/2B-1/2C+3/4D+3/4E+3/4F-G-H-I+1/4J+1/4K+1/4L 艮震巽离=1 +A+B+C-1/4D-1/4E-1/4F-1/2G-1/2H-1/2I+3/4J+3/4K+3/4L 坤兑乾坎=-1 -A-B-C+1/4D+1/4E+1/4F+1/2G+1/2H+1/2I-3/4J-3/4K-3/4L
In the format intends to constant items out of independence, so that you can see the back of the item is how to match, the same will be innate days after the change is also discharged:
离乾艮震= 3/2 -1/2A-1/2B-1/2C+3/4D+3/4E+3/4F+1/4G+1/4H+1/4I+J+K+L 艮震离乾= 3/2 +1/4A+1/4B+1/4C+D+E+F-1/2G-1/2H-1/2I+3/4J+3/4K+3/4L 震离乾艮= 3/2 +3/4A+3/4B+3/4C+1/4D+1/4E+1/4F+G+H+I-1/2J-1/2K-1/2L 乾艮震离= 3/2 +A+B+C-1/2D-1/2E-1/2F+3/4G+3/4H+3/4I+1/4J+1/4K+1/4L
Compare to get interesting results:
坎艮震巽= -1 -1/4A-1/4B-1/4C-1/2D-1/2E-1/2F+3/4G+3/4H+3/4I-J-K-L 离坤兑乾= 1 +1/4A+1/4B+1/4C+1/2D+1/2E+1/2F-3/4G-3/4H-3/4I+J+K+L 艮震离乾= 3/2 +1/4A+1/4B+1/4C+D+E+F-1/2G-1/2H-1/2I+3/4J+3/4K+3/4L 震巽离坤=-(1/2) -3/4A-3/4B-3/4C+D+E+F-1/4G-1/4H-1/4I-1/2J-1/2K-1/2L 兑乾坎艮= 1/2 +3/4A+3/4B+3/4C-D-E-F+1/4G+1/4H+1/4I+1/2J+1/2K+1/2L 震离乾艮= 3/2 +3/4A+3/4B+3/4C+1/4D+1/4E+1/4F+G+H+I-1/2J-1/2K-1/2L 巽离坤兑=1/2 +1/2A+1/2B+1/2C-3/4D-3/4E-3/4F+G+H+I-1/4J-1/4K-1/4L 乾坎艮震=-(1/2) -1/2A-1/2B-1/2C+3/4D+3/4E+3/4F-G-H-I+1/4J+1/4K+1/4L 离乾艮震= 3/2 -1/2A-1/2B-1/2C+3/4D+3/4E+3/4F+1/4G+1/4H+1/4I+J+K+L 艮震巽离=1 +A+B+C-1/4D-1/4E-1/4F-1/2G-1/2H-1/2I+3/4J+3/4K+3/4L 坤兑乾坎=-1 -A-B-C+1/4D+1/4E+1/4F+1/2G+1/2H+1/2I-3/4J-3/4K-3/4L 乾艮震离=3/2 +A+B+C-1/2D-1/2E-1/2F+3/4G+3/4H+3/4I+1/4J+1/4K+1/4L
Leave a Reply