见到知乎上有一个解释说,基础形式实际上类似于差分放大,很有道理。
假如: F'(5)=5.1 从5到5.1的变化率是极低的,因为5的基数太大,所以可以进行拆分:
H(5)=5.1, H(5)=5+F(5), F(5)=0.1 此时由于在拆分项中0变成0.1,这个变化率就达到了10%,便放大了这种效果。 因为神经网络不能很好辨识出这种拆分,所以需要人工设计结构进行辅助,
一般理论上认为网络层数越多,提取细节与抽象能力越丰富,然而实际层数迭代多了,会出现梯度爆炸或梯度弥散 ,这可以通过通过正则化解决。
但即使解决了这个问题,仍然会有退化问题,即层数多了后,出现准确率反而下降的情况。
这里有一个变化的技巧就是,在 H(x) = F(x) + x 时,当F(x)=0时, 显然H(x) = x,如果f(x)越来越趋近于0,则h(x)越来越趋进x
所以可以构造这样的形式: 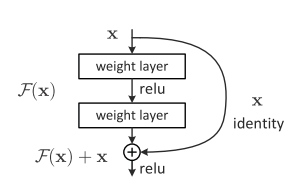
所以,x可以直接跳两层作为输入,因为h(x)=x,f(x)这里当然不会等于0,但是可以通过relu使得矩阵中尽量多的地方变成0,从而实现残差放大。
X如何变化是不清楚的,因为它本来就是一个需要求的值,但这里可以直接采用X的原值,因为是如果改变了X值,那么就会破坏掉残差对应的原来的X结构,因为这里的残差实际上不是差分,而只是一个通过训练后才有可能不断向差分靠拢的值。
发表评论