如果把量子操作视作类似电路那样的话,因为单个量子比特不但有阴态还有阳态以及混合态,要实现可控性可以利用其中的相互作用来实现控制。
所以可以设计进行逻辑控制的门,那么需要操作的最基础为四种情况:不变,翻转,等0,等1。
简单说操作其实就是控制一个量子态转换成另外一个量子态,这个过程可以称为演化,而演化,实际上就在Hilbert空间中的旋转。
而在Hilbert空间中的旋转可以使用矩阵来进行,而矩阵使用的是酉矩阵,也叫酉变换,所以这里可以叫作U操作。
酉变换特点就是能够保证内积、长度、向量夹角、形状四者不变的进行下进行变换。
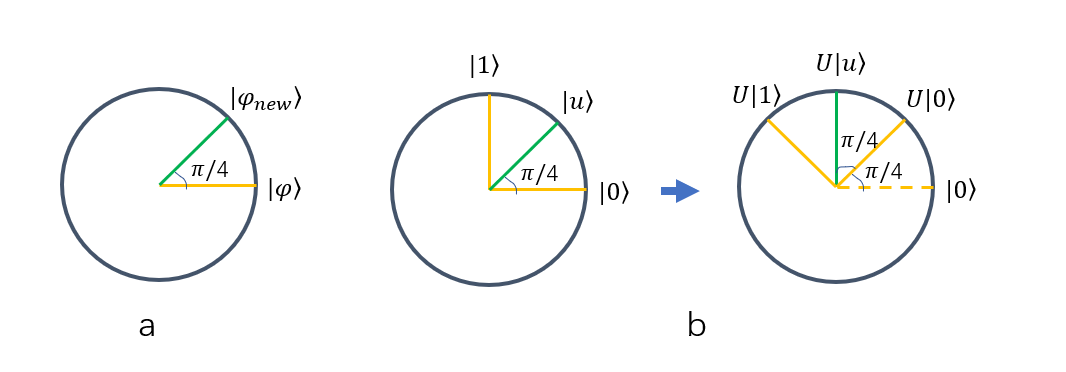
如图中所示,如|0>、|1>、|u⟩ 三个态,对它们进行U操作后,变换出来的结果,并不会改变|0>、|1>、|u⟩ 之间的关系。
所以比如\((| 0\rangle, | 1\rangle)=0\)时,很显然 \((U| 0\rangle, U| 1\rangle)=0\),所以可以放心大胆的进行U操作。
单个量子比特用一个2*1的向量可以表达,而一个单量子比特门,就成了一个2*2的向量,|0⟩ 变到 U|0⟩ 这个过程,相当于把 [1,0] 变成了 \(\left[ \begin{array}{}{\frac{1}{\sqrt2}} \ {\frac{1}{\sqrt2}}\end{array}\right]\),这里需要理解的就是,这里的值发生了变化,然而它还是等价的,是因为它参考系发生了变化,所以看起来值也就发生了变化,而U操作特点是可逆的,所以同样也可以反向将U|0⟩变换成|0>。
这类似于比如在一个固定的二元的线性方程上,在等号左右两侧同时乘以一个倍率,而X与Y的值仍然能保持不变一样。
这些细节其实即使是不知道也没有大问题,只用简单的知道通过符合规范的矩阵可以进行量子操作就可以了。
那么可以对量子比特进行什么操作?最最基础的有以下几种:
第一个是X门,作用就是翻转,即把|0>变成|1>,或反之,用四象表达就是把阴态变成阳态,或把阳态变成阴态,通过这个矩阵便能够实现,这个称为X门,也就是阴阳转换用的门。
\(X=\left[ \begin{array}{}{0} &{1} \\ {1}&{0} \end{array}\right]\)第二个是Y门,它的特点是对i进行操作
\(Y=\left[ \begin{array}{}{0} &{-i} \\ {i}&{0} \end{array}\right]\)突然冒出来向量i,会有些无可适从,不知道它表达的是什么,其实这里相当于一种简化,实际上:
\(i=\begin{bmatrix} {\frac{1} {\sqrt{2}}} \\ {\frac{1} {\sqrt{2}}}\\ \end{bmatrix}\)第三个是Z门,Z门也叫相位翻转门,它可以把 |+⟩ 变成 |−⟩ , −|1⟩ 变成 |1⟩。
\(Z=\left[ \begin{array}{}{1} &{0} \\ {0}&{-1} \end{array}\right]\)第四种是H门,它的作用非常重要,它可以把 |1⟩ 变成 |−⟩, 把|0⟩ 变成 |+⟩ ,它的表达是:
\(H=\left[ \begin{array}{}{\frac{1}{\sqrt2}} &{\frac{1}{\sqrt2}} \\ {\frac{1}{\sqrt2}}&{-\frac{1}{\sqrt2}} \end{array}\right]\)举例来说,比如现在有一个|1>,称为阳态,要它变成叠加态,可以使用H门操作它,然后就变成了|->,如果对它进行一个Z操作,它就变成了|+>
那么|+>及|->是代表的什么含义?在狄拉克定义中,是这样的:
\(|+\rangle=\frac{1} {\sqrt{2}} |(|0\rangle+|1\rangle)\) \(|-\rangle=\frac{1} {\sqrt{2}} |(|0\rangle-|1\rangle)\)为什么会有这种看起来奇怪的表达,因为波可叠加与干涉是有方向的,以需要有正负号出现,可以相象一下有叠加与消除,有波峰波谷以及其它部分
为了以示区别,取其阳升之故,可以将|+>称之为青龙,而取阳降之故,|->称之为白虎态。
Leave a Reply